Author's Note: Commercial products are identified
as examples. Such identification does not imply recommendation or endorsement
by the National Institute of Standards and Technology, nor does it imply
that they are necessarily the best available for the purpose.
The present paper gives an overview of the CALPHAD method and recent progress made. A brief history is given then the scope of phase diagram calculations is described. Thermodynamic descriptions most commonly used in the Calphad method are described and the methods used to obtain the numerical values for these descriptions are outlined. Extrapolation to higher-component systems is explained and recent progress in the quality of assessments is demonstrated. A brief overview of available computer software tools and databases is given. Finally, several applications of phase diagrams calculations are demonstrated.
Introduction
Phase diagrams are visual representations of the state of a material as a function of temperature, pressure and concentrations of the constituent components and are, therefore, frequently hailed as basic blueprints or roadmaps for alloy design, development, processing and basic understanding. The importance of phase diagrams is also reflected by the publication of such handbooks as "Binary Alloy Phase Diagrams"1, "Phase Equilibria, Crystallographic and Thermodynamic Data of Binary Alloys"2, "Phase Equilibrium Diagrams"3 which continues "Phase Diagrams for Ceramists"4, "Handbook of Ternary Alloy Phase Diagrams"5 and "Ternary Alloys"6.
The state of a two-component material at constant pressure can be presented
in the well known graphical form of binary phase diagrams. For three-component
materials an additional dimension is necessary for a complete representation.
Therefore, ternary systems are usually presented by a series of sections
or projections. Due to their multidimensionality the
interpretation of the diagrams of more complex systems can be quite cumbersome
for an occasional user of these diagrams. For systems with more than 3
components, the graphical representation of the phase diagram in a useful
form becomes not only a challenging task but is also hindered by the lack
of sufficient experimental information. However, the difficulty of graphically
representing systems with many components is irrelevant for the calculation
of phase diagrams. Such calculations can be customized for the materials
problem of interest.
History
While it is only modern developments in modeling and computational technology that have made computer calculations of multicomponent phase equilibria a realistic possibility today, the correlation between thermodynamics and phase equilibria was established more than a century ago by J.W. Gibbs. Hertz7 has summarized the ground breaking work of Gibbs. Although the mathematical foundation had been laid, more than 30 years passed before J.J. van Laar8 published his mathematical synthesis of hypothetical binary systems. To describe the solution phases van Laar used concentration dependent terms which Hildebrand9 called regular solutions. More than 40 years have had passed when J.L. Meijering published his calculations of miscibility gaps in ternary10 and quaternary solutions11. Shortly afterwards Meijering applied this method to the thermodynamic analysis of the Cr-Cu-Ni system12. Simultaneously Kaufman and Cohen13 applied thermodynamic calculations in the analysis of the martensitic transformation in the Fe-Ni system. Kaufman continued his work on the calculation of phase diagrams, including the pressure dependence. In 1970 Kaufman and Bernstein14 summarized the general features of the calculation of phase diagrams and also gave listings of computer programs for the calculation of binary and ternary phase diagrams, thus laying the foundation for the CALPHAD method (CALculation of PHAse Diagrams). In 1973 Kaufman organized the first project meeting of the international CALPHAD group. Since then the CALPHAD group grown consistently larger.
Another important paper on the calculation of phase equilibria was also
published in the fifties. In his paper Kikuchi15 described a
method to treat order/disorder phenomena. This method later became known
as the "Cluster Variation Method" (CVM) and is extensively used in conjunction
with first principles calculations. Although these calculations are computationally
very intensive, enormous progress in algorithms and computer speed has
been made in recent years. The predicted phase diagrams are generally topologically
correct but they currently still lack sufficient accuracy for practical
applications. de Fontaine16 gives an extensive review of these
calculations.
Scope of Phase Diagram Calculations
In order to overcome the problem of the multidimensionality posed by a system with many components, alternate methods are frequently used to represent the necessary phase diagram information. With stainless steel alloys, for example, the complexity is frequently reduced by expressing the compositions of the ferrite-stabilizing elements as "Cr equivalents" and the austenite-stabilizing elements as "Ni equivalents"17. The sums of the Cr and Ni equivalents are used to predict the phases expected in the final alloy. It should be noted that approximations like these are limited to the composition regime for which they were derived. Another example is the PHACOMP method18 used to predict detrimental TCP (topological close packed) phases in superalloys. This method is based on the theory that each element has a specific electron hole number and that the average electron hole number is correlated to the TCP phases in an alloy. Although this method works very well for Ni-based superalloys, special corrections are required with other superalloys, and it may not be easily applied to other alloy families. The CALPHAD method, on the other hand, is based on the minimization of the free energy of the system and is, thus, not only completely general and extensible, but also theoretically meaningful.
The experimental determination of phase diagrams is a time consuming and costly task. This becomes even more pronounced as the number of components increases. The calculation of phase diagrams reduce the effort required to determine equilibrium conditions in a multicomponent system. A preliminary phase diagram can be obtained from extrapolation of the thermodynamic functions of constituent subsystems. This preliminary diagram can be used to identify composition and temperature regimes where maximum information can be obtained with minimum experimental effort. This information can then be used to refine the original thermodynamic functions.
Numerical phase diagram information is also frequently needed in other modeling efforts. Even though phase diagrams represent thermodynamic equilibrium, it is well established that the phase equilibria can be applied locally (local equilibrium) to describe the interfaces between phases. In such cases only the concentrations at this interface are assumed to obey the requirements of thermodynamic equilibrium. Thermodynamic modeling of phase diagrams and kinetic modeling have been successfully coupled for a variety of processes, such as carburizing/nitriding19,20, diffusion couples21-23, dissolution of precipitates24,25 and solidification26,27. Phase equilibrium calculations can not only give the phases present and their compositions but also provide numerical values of enthalpy contents, temperature and concentration dependence of phase boundaries for coupling of microscopic and macroscopic modeling. Banerjee et al.28 give an example of such a coupling of phase equilibria calculations and solidification micromodels in a macroscopic heat and fluid flow analysis of a casting.
In recent years the expression "computational thermodynamics" is frequently
used in place of "calculation of phase diagrams". This reflects the fact
that the phase diagram is only a portion of the information that can be
obtained from these calculations.
Thermodynamic Descriptions and Models
For the calculation of phase equilibria in a multicomponent system,
it is necessary to minimize the total Gibbs energy, G, of all the
phases that take part in this equilibrium:
| (1) |
A thermodynamic description of a system requires assignment of thermodynamic
functions for each phase. The CALPHAD method employs a variety of models
to describe the temperature, pressure and concentration dependencies of
the free energy functions of the various phases. The contributions to the
Gibbs energy of a phase can be written:
| (2) |
The temperature dependence of the concentration terms of GT is usually expressed as a power series of T:
| (3) |
For multicomponent systems it has proven useful to distinguish three
contributions from the concentration dependence to the Gibbs energy of
a phase, G:
| (4) |
The Gibbs energy of a binary stoichiometric phase is given by:
| (5) |
Binary solution phases, such as liquid and disordered solid solutions,
are described as random mixtures of the elements by a regular solution
type model:
| (6) |
The most complex and general model is the sublattice model frequently
used to describe ordered binary solution phases. The basic premise for
this model is that a sublattice is assigned for each distinct site in the
crystal structure. For example, the CsCl (B2) structure consists of two
sublattices, one of which is occupied predominantly by Cs atoms and the
other by Cl atoms. An ordered binary solution phase with two sublattices
that exhibits substitutional deviation from stoichiometry can be described
by the expression:
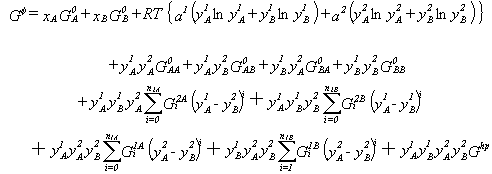 |
(7) |
It should be noted that Eqs. (5) and (6) are in fact special cases of Eq. (7). Equation (7) reduces to Eq. (6) if only one sublattice is considered or Eq. (5) if only one species is considered on each of the two sublattices. The generality of the sublattice description allows formulation of a general description for multi-component phases that can easily be computerized. Lukas et al.35 give an example of such a description.
From the condition that the Gibbs energy at thermodynamic equilibrium
reveals a minimum for given temperature, pressure and composition, J.W.
Gibbs derived the well known equilibrium conditions that the chemical potential,
µn, of each component, n, is the same in
all phases, :
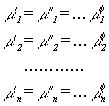 |
(8) |
| (9) |
Determination of the Coefficients
The coefficients of the Gibbs energy functions are determined from experimental
data for each system. In order to obtain an optimized set of coefficients,
it is desirable to take into account all types of experimental data, e.g.
phase diagram, chemical potential and enthalpy data. The coefficients can
be determined from the experimental data by a trial and error method or
mathematical methods. The trial and error method is only feasible if few
different data types are available. This method becomes increasingly cumbersome
as the number of components and/or number of data types increases. In this
case mathematical methods, such as the least squares method of Gauss42,
the Marquardt method43 or Bayesian estimation method44,
are more efficient. The determination of the coefficients is frequently
called "assessment" or "optimization" of a system.
Higher-Component Systems
A higher-component system can be calculated from thermodynamic extrapolation
of the thermodynamic excess quantities of the constituent subsystems. Several
methods exist to determine the weighting terms used in such an extrapolation
formula. Hillert45 analyzed various extrapolation methods and
recommended the use of Muggianu's method46 since it can easily
be generalized. The Gibbs energy of a ternary solution phase determined
by extrapolation of the binary energies using Muggianu's method is given
by:
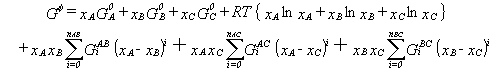 |
(10) |
The usual strategy for assessment of a multicomponent systems is shown
in Fig. 1. First, the thermodynamic descriptions of the constituent binary
systems are derived. Thermodynamic extrapolation methods are then used
to extend the thermodynamic functions of the binaries into ternary and
higher order systems. The results of such extrapolations can then be used
to design critical experiments. The results of the experiments are then
compared to the extrapolation and, if necessary, interaction functions
are added to the thermodynamic description of the higher order system.
As mentioned previously, the coefficients of the interaction functions
are optimized on the basis of these data. In principle, this strategy is
followed until all 2, 3, ... n constituent systems of a n-component
system have been assessed. However, experience has shown that, in most
cases, no, or very minor, corrections are necessary for reasonable prediction
of quaternary or higher component systems. Since true quaternary phases
are rare in metallic systems, assessment of most of the ternary constituent
systems is often sufficient to describe a n-component system.
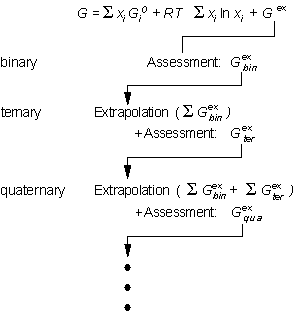 |
Figure 1: CALPHAD methodology. The assessed excess Gibbs energies of the constituent subsystems are for extrapolation to higher component system. |
Improved Capabilities
One goal of the CALPHAD group is to generate descriptions of binary,
ternary and quaternary systems that can be used for the construction of
thermodynamic databases. Thermodynamic databases of multicomponent system
require consistency of the model descriptions and the parameters used.
With the constant improvement of computational technology, the use of more
realistic models, such as the sublattice model description, becomes feasible.
This allows more accurate descriptions of complex systems and makes it
desirable to reassess systems which have been previously assessed.
The progress that has been made with these reassessments is shown in
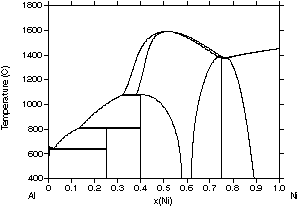
Fig. 2 for the Al-Ni system, a basic system for superalloys. In the first
assessment of Kaufman and Nesor47, shown in Fig. 2(a), the phases
were either described as disordered solution phases (liquid, (Al), (Ni)
and AlNi) or stoichiometric compounds (Al3Ni, Al3Ni2
and AlNi3). The (Al) and (Ni) phases were described as one phase
since they both have the fcc structure. Although the general topology of
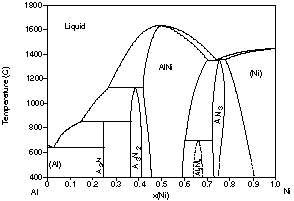
the experimentally determined phase diagram48 (Fig. 2(d)) is
reproduced, major differences occur for the equilibria involving the Al3Ni2
and AlNi phases. These differences are at least partially a result of ignoring
the homogeneity range of the Al3Ni2 phase and not
considering the fact that AlNi is an ordered phase with CsCl structure.
 a a |
 b b |
|
 c c |
 d d |
|
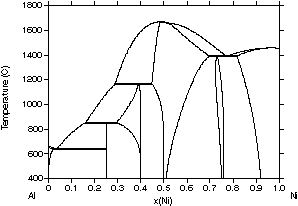
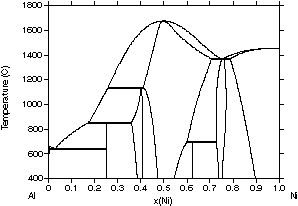
| Figure 2: Different assessments of the Al-Ni system showing the progress made with the CALPHAD method. (a) 1978 assessment by Kaufman and Nesor [78Kau], (b) 1988 assessment by Ansara et al. [88Ans], (c) 1997 assessment by Ansara et al. [97Ans] and (d) the evaluated experimental diagram [93Oka]. | ||
A disadvantage of this iterative process with improved descriptions
is that the descriptions used in previous assessments may be incompatible
with newer assessments based on recently developed model descriptions.
Despite this, significant progress has been made in recent years and an
increasing number of databases have become available for multicomponent
systems.
Computer Software Tools and Databases
A variety of software packages can be used for the calculation of phase diagrams making it is impossible to list all of them. Frequently used software packages are ChemSage49, the so-called Lukas programs35,42, MTDATA50 and Thermo-Calc51. Although, all of these software packages can be used for the calculation of phase equilibria, their features and user interfaces differ. Most of the model descriptions used for alloy and ceramic systems are common to all these programs. However, not every package has other specific model descriptions, for example, models for aqueous or polymer solutions. Another important feature of these software packages is the availability of a module for the optimization of the Gibbs energy functions. Such optimizing modules are available with ChemSage52, the Lukas programs42 and Thermo-Calc53.
The development of increasingly user friendly computer interfaces, very often in conjunction with programs for special tasks, such as the ETTAN PC-Windows interface54 for Thermo-Calc or the SCHEIL and LEVER programs55, makes phase diagram information more accessible for the non-expert user. For these applications the user needs only to supply a bulk composition and temperature limits for the calculation and the programs generate the remaining conditions that are needed for the calculation.
For the incorporation of phase equilibria calculations into micromodeling, such as the modeling of diffusion processes, an interface must be created in which the important variables are transferred from one computer code segment to another. For the simulation of diffusional reactions, the software package Thermo-Calc51 has been interfaced with the package DICTRA56. A general interface (TQ interface) is available for Thermo-Calc and ChemSage57. Banerjee et al.28 used another, fairly simple interface for solidification micromodeling.
Several thermodynamic databases have been constructed from the assessments of binary, ternary and quaternary systems. For the description of commercial alloys is quite likely that at least a dozen elements need to be considered. The number of constituent subsystems of a n-component system is determined by the binomial coefficient (nk), where k is the number of components in the subsystem. A 12-component systems consists accordingly of 66 binary, 220 ternary and 495 quaternary subsystems. These numbers suggest that is impossible to obtain descriptions of all the subsystems in reasonable time. However, as mentioned previously, only rarely are quaternary excess parameters needed. If the database is for base element X, it is sufficient to consider only the X-based ternary systems, considerably reducing the number of needed assessments. Also, if more than one element occurs only in fairly small quantities in the alloy family of interest then assessments for binary systems containing only these elements or ternary systems with two or three of these elements are generally not very important for obtaining correct predictions. Based on this, databases have been developed for various commercial alloy systems58,59. However, because software packages assume different computer file formats for the databases, care must be taken to insure compatibility between database and program package.
A review of fully integrated thermochemical database systems which were
available in 1990 is given by Bale and Eriksson60. Since then,
their review has been complemented by a web site61.
Application Examples
In recent years, the application of phase diagram information obtained from calculations to practical processes has increased significantly. Extensive collections of examples can be found in books: "User Applications of Alloy Phase Diagrams"62, "User Aspects of Phase Diagrams"63 and "The SGTE Casebook, Thermodynamics at work"64. In the following, a few examples will be given for solidification processes.
As has been already mentioned, extrapolation to higher-component systems
is one of the staples of the CALPHAD since it provides information where
otherwise only educated guesses could be used. When alloys of the Sn-Ag-Bi
system were considered as candidate alloys for lead-free solders no phase
diagram information for the liquid phase could be found. Kattner and Boettinger65
extrapolated the descriptions of the binary systems to calculate the solidus
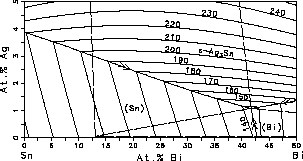
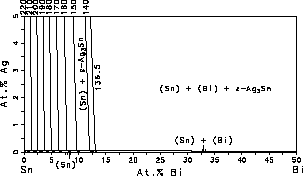
and liquidus surfaces of the Sn-rich corner, Fig. 3. It can be seen from
Fig. 3 that the Ag-rich side of the eutectic troughs should be avoided
because the liquidus temperature increases significantly with increasing
Ag-concentration. Fig. 3(a) and Fig. 3(b) can be used to identify composition
regimes where the freezing range is suitable for solder applications.
 a a |
 b b |
|
| Figure 3: Sn-rich corner of the Sn-Bi-Ag system with isotherms. (a) Liquidus surface, the dashed lines are the boundaries of the three phase equilibria at the eutectic temperature. (b) Solidus surface. | ||
 a a |
 b b |
|
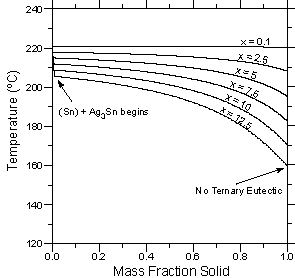
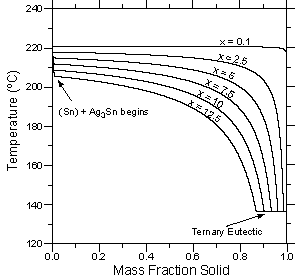
| Figure 4: Temperature vs. calculated fraction solid curves for six alloys with the composition Sn - 3.5 wt.% Ag - x wt.% Bi. (a) Lever rule calculations. (b) Scheil calculations. | ||
 a a |
 b b |
|
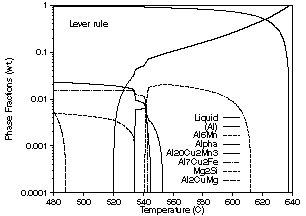
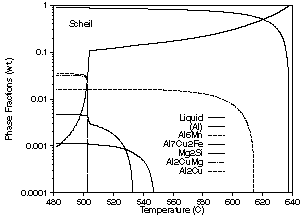
| Figure 5: Phase fraction vs. temperature curves for solidification of an alloy with the composition 0.21 wt.% Si, 0.23 wt.% Fe, 4.44 wt.% Cu, 0.55 wt.% Mn 1.56 wt.% Mg, 0.05 wt.% Zn and the remainder Al. (a) Lever rule calculation. (b) Scheil calculation. | ||
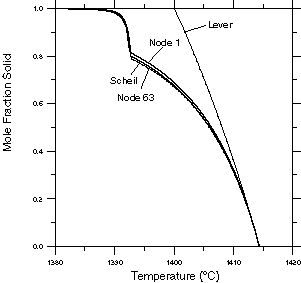 |
Figure 6: Fraction solid vs. local temperature curves for the two nodes from the casting simulation compared to the curves obtained from Scheil and lever rule solidification calculations. |
Conclusion
Enormous progress has been made in the calculation of phase diagrams during the past 30 years. This progress will continue as model descriptions are improved and computational technology advances. The progress of the recent years can be summarized:
The model descriptions used in the CALPHAD method are constantly improved, allowing assessments which reproduce even complex diagrams well.
A large number of systems have been assessed, allowing the construction of databases for calculating phase diagrams of complex commercial alloys.
The user interfaces of the computer programs are becoming more user friendly, allowing the non-expert user easy access to phase diagram information.
The calculation of phase diagrams has been successfully coupled with
the modeling of kinetic processes.
Acknowledgement
The different versions of the Al-Ni phases diagram in Fig. 2 were calculated
with the Thermo-Calc package. The remaining calculations were carried out
with the original Lukas programs (Fig. 3) or with programs that were using
modified code (Figs. 4-6). The author thanks H.L. Lukas, Max-Planck-Institut
of Metallforschung (Stuttgart, Germany) for providing his computer programs
and N. Saunders, ThermoTech Ltd. (Surrey, United Kingdom) for providing
the Al-DATA database used for the calculation shown in Fig. 5.
References
1. "Binary Alloy Phase Diagrams", 2nd Ed., Vol. 1-3, Ed. in Chief: T.B. Massalski, ASM International, Materials Park, OH, 1990
2. B. Predel, "Phase Equilibria, Crystallographic and Thermodynamic Data of Binary Alloys", Vol. 5, Subvol. a-g, Ed. in Chief O. Madelung, Landolt-Börnstein, New Series, Springer, Berlin, Germany, 1991-1997; onward
3. "Phase Equilibria Diagrams", Vol. IX-XII, Compiled in the Ceramics Division of NIST, The American Ceramic Society, Westerville, OH, 1992-1996; onward
4. "Phase Diagrams for Ceramists", Vol. I-VIII, Compiled in the Ceramics Division of NIST, The American Ceramic Society, Westerville, OH, 1964-1990
5. P. Villar, A. Prince and H. Okamoto, "Handbook of Ternary Alloy Phase Diagrams", Vol. 1-10, ASM International, Materials Park, OH, 1995
6. "Ternary Alloys: A comprehensive Compendium of Evaluated Constitutional Data & Phase Diagrams", Vol. 1-15, Eds.: G. Petzow and G. Effenberg, VCH Verlagsgesellscahft, Weinheim, Germany, 1988-1995; onward
7. J. Hertz, J. Phase Equilibria, 13 (1992) 450-458
8. J.J. van Laar, Z. phys. Chem., 63 (1908) 216-253, 64 (1908) 257-297
9. J.H. Hildebrand, J. Amer. Chem. Soc., 51 (1929) 66-80
10. J.L. Meijering, Philips Res. Rep., 5 (1950) 333-356, 6 (1951) 183-210
11. J.L. Meijering and H.K. Hardy, Acta Metall., 4 (1956) 249-256
12. J.L. Meijering, Acta Metall., 5 (1957) 257-264
13. L. Kaufman and M. Cohen, J. Metals, 8 (1956) 1393-1401 (Trans. AIME, 206)
14. L. Kaufman and H. Bernstein, "Computer Calculation of Phase Diagrams with Special Reference to Refractory Metals", Academic Press, New York, NY, 1970
15. R. Kikuchi, Phys. Rev., 81 (1951) 988-1003
16. D. de Fontaine, Solid State Physics, 47 (1994) 33-176
17. E.A. Schoefer, Weld. J., Res. Suppl., 39 (1974) s10-s12
18. C.T. Sims, "Prediction of Phase Composition" in "Superalloys II", Eds.: C.T. Sims, N.S. Stoloff and W.C. Hagel, John Wiley & Sons, New York, NY, 1987, 217-240
19. A. Engstrom, L. Höglund, and J. Ågren, Metall. Mater. Trans. A, 25A (1994) 1127-1134
20. H. Du and J. Ågren, Metall. Mater. Trans. A, 27A (1996) 1073-1080
21. M. Kajihara, C. Lim. and M. Kikuchi, ISIJ Inter., 33 (1993) 498-507
22. A. Engstrom, J. E. Morral and J. Ågren, Acta mater., 45 (1997) 1189
23. T. Helander and J. Ågren, Metall. Mater. Trans. A, 28A (1997) 303-308
24. J. Ågren, Scand. J. Met., 19 (1990) 2-8
25. Z.-K. Liu, L. Höglund, B. Jönsson and J. Ågren, Metall. Trans. A, 22A (1991) 1745-1752
26. T. Kraft, M. Rettenmayr and H.E. Exner, Modelling Simul. Mater. Sch. Eng. 4 (1996) 161-177
27. N. Saunders, Proc. 4th Decennial Int. Conf. Solidification Processing, Eds.: J. Beech and H. Jones, University of Sheffield, UK, 1997, 362-366
28. D.K. Banerjee, M.T. Samonds, U.R. Kattner and W.J. Boettinger, Proc. 4th Decennial Int. Conf. Solidification Processing, Eds.: J. Beech and H. Jones, University of Sheffield, UK, 1997, 354-357
29. A.T. Dinsdale, CALPHAD, 15 (1991) 317-425
30. M. Hillert and L.-I. Staffansson, Acta Chem. Scand., 24 (1970) 3618-3626
31. F. Sommer, Z. Metallkd., 73 (1982) 72-76
32. C. Wagner und W. Schottky, Z. phys. Chem., B11 (1930) 163-210
33. W.L. Bragg and E.J. Williams, Proc. Royal Soc. A, London, 145 (1934) 699-730; 151 (1935) 540-566
34. O. Redlich and A.T. Kister, Indust. Eng. Chem., 40 (1948) 345-348
35. H.L. Lukas, J. Weiss and E.-Th. Henig, CALPHAD 6 (1982) 229-251
36. B. Sundman and J. Ågren, J. Phys. Chem. Solids, 42 (1981) 297-301
37. J.-O. Andersson, A. Fernández Guillermet, M. Hillert, B. Jansson and B. Sundman, Acta metall., 34 (1986) 437-445
38. I. Ansara, B. Sundman and P. Willemin, Acta metall., 36 (1988) 977-982
39. I. Ansara, N. Dupin, H.L. Lukas and B. Sundman, J. Alloys Compd., 247 (1997) 20-30
40. S.-L. Chen, C.R. Kao and Y.A. Chang, Intermetallics, 3 (1995) 233-242
41. M. Hillert, Physica 103B (1981) 31-40
42. H.L. Lukas, E.-Th. Henig and B. Zimmermann, CALPHAD 1 (1977) 225-236
43. D.W. Marquardt, J. Soc. Indust. Appl. Math., 11 (1963) 431-441
44. E. Königsberger, CALPHAD, 15 (1991) 69-78
45. M. Hillert, CALPHAD, 4 (1980) 1-12
46. Y.-M. Muggianu, M. Gambino et L.P. Bros, J. Chim. Phus. 72 (1975) 85-88
47. L. Kaufman and H. Nesor, CALPHAD, 2 (1978) 325-348
48. H. Okamoto, J. Phase Equilibria, 14 (1993) 257-259
49. G. Eriksson and K. Hack, Metall. Trans.B, 21B (1990) 1013-1023
50. R.H. Davies, A.T. Dinsdale, J.A. Gisby, S.M. Hodson and R.G.J. Ball, in "Applications of Thermodynamics in the Synthesis and Processing of Materials", Eds. P. Nash and B. Sundman, TMS, Warrendale, PA, 1995, 371-384
51. B. Sundman, B. Jansson and J.-O. Andersson, CALPHAD, 9 (1985) 153-190
52. E. Königsberger and G. Eriksson, CALPHAD, 19 (1995) 207-214
53. B. Sundman, in "User Aspects of Phase Diagrams" Ed. F.H. Hayes, Institute of Metals, London, UK 1991, 130-139
54. B. Sundman, "Thermo-Calc Newsletter No. 18", Royal Institute of Technology, Stockholm, Sweden 1995
55. U.R. Kattner, W.J. Boettinger, S.R. Coriell, Z. Metallkd. 87 (1987) 522-528
56. J. Ågren, ISIJ International, 32 (1992) 291-296
57. G. Eriksson, H. Sippola and B. Sundman, CALPHAD, 18 (1994) 345-345
58. SGTE Solution Database: SGTE, St. Martin d'Hères, France
59. Al-DATA, Fe-DATA, Ni-Data, Ti-DATA: ThermoTech Ltd., Surrey, UK
60. C.W. Bale and G. Eriksson, Canad. Metall. Quarterly, 29 (1990) 105-132
61. C.W. Bale, "Web Sites in Inorganic Chemical Thermodynamics", http://www.crct.polymtl.ca/fact/websites.htm
62. "User Applications of Alloy Phase Diagrams", Ed. L. Kaufman, ASM International, Metals Park, OH, 1987
63. "User Aspects of Phase Diagrams", Ed. F.H. Hayes, The Institute of Metals, London, UK, 1991
64. "The SGTE Casebook, Thermodynamics at work", Ed. K. Hack, The Institute of Metals, London, UK, 1996
65. U.R. Kattner and W.J. Boettinger, J. Electron. Mater., 23 (1994) 603-610
66. N. Saunders, Materials Science Forum,
217-222, (1996), 667-672